Simulação integrativa do comportamento mecânico de peças de borracha moldadas por injeção

1 SIGMA Engineering GmbH, Aachen, Germany
G.Weinhold@magmasoft.de
F.Leins@magmasoft.de
2 Polymer Competence Center Leoben GmbH, Leoben, Austria
michaela.hornbachner@pccl.at
roman.kerschbaumer@pccl.at

A simulação de processos com Sigmasoft é uma forma bem estabelecida de encurtar custos e tempo no caminho desde a primeira ideia de uma peça de borracha até à produção em massa. Por seu lado, a análise estrutural das peças finais através do Método dos Elementos Finitos é essencial para a previsão do comportamento do produto sob carga. Ambas as abordagens são determinantes para a qualidade final das peças de borracha moldadas por injeção.

A compreensão de todo o processo de produção é determinante para a qualidade final e eficiência económica das peças fabricadas com elastómeros. No entanto, a produção e a utilização são duas visões separadas do mesmo produto. Isto significa que são necessárias duas abordagens distintas de simulação: simulação de processos e análise estrutural.

Um processo de moldação por injeção é estabelecido de modo a que a cavidade possa ser preenchida homogeneamente com uma pressão de injeção razoável e que seja atingido um certo grau de cura. A análise estrutural é baseada em parâmetros mecânicos, tais como o módulo de Young ou a rigidez dinâmica. Os resultados da simulação do processo não estão normalmente correlacionados com as propriedades mecânicas, pelo que a informação da simulação da moldação por injeção é inacessível para a análise estrutural. Isto resulta normalmente na assunção de parâmetros mecânicos homogéneos para a análise estrutural, o que constitui uma grande simplificação.

Nesta contribuição será demonstrado que o processo de produção está a influenciar significativamente as propriedades mecânicas da peça final. Será mostrada uma estratégia experimental para caracterizar a ligação entre o processo de produção e as propriedades finais. Além disso, será apresentada uma nova abordagem para modelar as propriedades mecânicas da peça final com base numa simulação do processo de produção.

O objetivo das medições é caracterizar a influência do processo de produção sobre as propriedades mecânicas da peça final em condições padrão. Por conseguinte, as amostras são produzidas com diferentes graus de cura e a temperaturas constantes distintas. Um molde de compressão é aquecido até à temperatura desejada e uma peça, ou seja, uma área interior: Ø70mm por 6,3mm de espessura, área exterior: Ø200mm por 2mm de espessura, é fabricado (ver Figura 1).

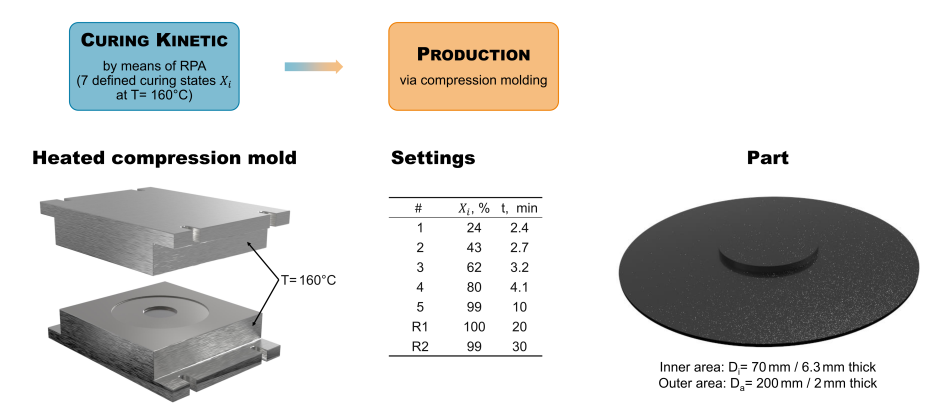
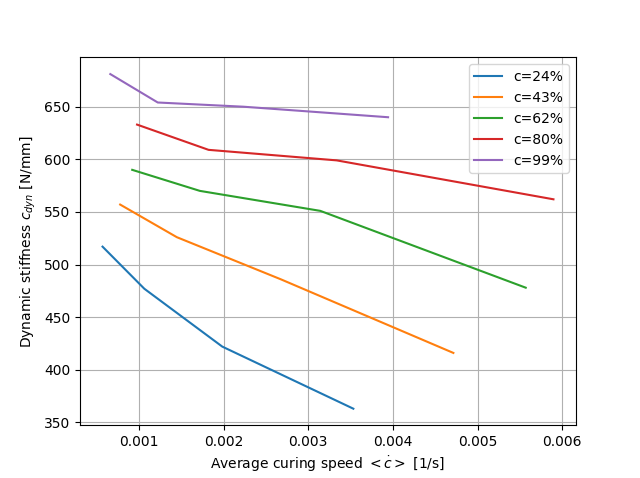
O tempo de cura necessário para atingir o grau de cura desejado é estimado a partir de experiências anteriores com equipamento de análise nos processos de borracha. A fim de parar a cura o mais rapidamente possível, a peça é rapidamente arrefecida em água gelada. Este procedimento é repetido três vezes para cada grau de cura e temperatura desejados. Finalmente, no centro da peça, a rigidez dinâmica foi analisada com uma análise mecânica dinâmica não destrutiva em modo de compressão para temperaturas de produção constantes 140°C, 150°C, 160°C, e 170°C. Diferentes intervalos de tempo para a regulação da água gelada levam aos diferentes valores do grau de cura 24%, 43%, 62%, 80% e 99% (ver Figura 2 e Figura 3).

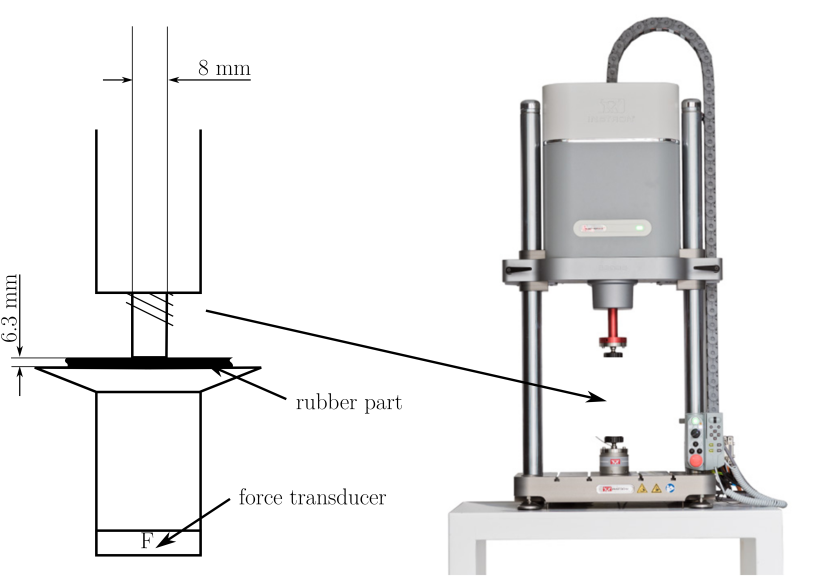
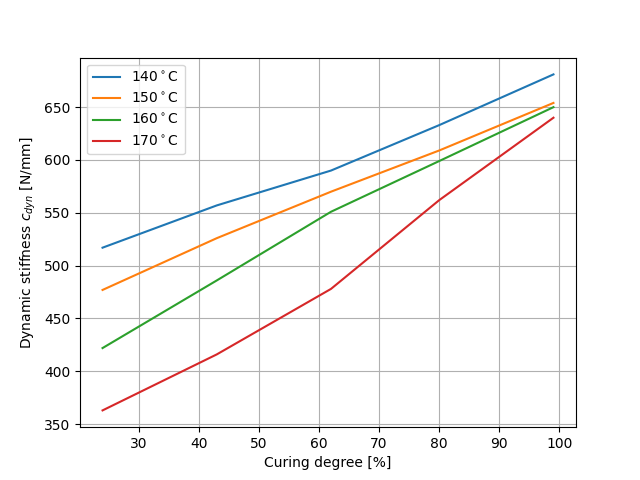
Pode observar-se que, com o aumento do grau de cura, a rigidez dinâmica também aumenta. Com o aumento da temperatura de produção, a rigidez dinâmica diminui. É de notar que a influência do grau de cura e a temperatura de produção são quase igualmente significativas. Uma peça curada até um grau de cura de 70% e uma temperatura de cura de 140°C tem a mesma rigidez dinâmica que uma peça curada até 90% a 170°C. Isto implica que a história da cura e o estado atual da cura são igualmente importantes.

Na peça, as temperaturas evoluem localmente, pelo que a hipótese de temperaturas constantes não é válida durante um processo de produção. A temperatura não é uma grandeza adequada para reproduzir a rigidez dinâmica. No entanto, uma temperatura mais elevada resulta numa reação de cura mais rápida. Assim, a velocidade média de cura ⟨ċ⟩ é introduzida¹

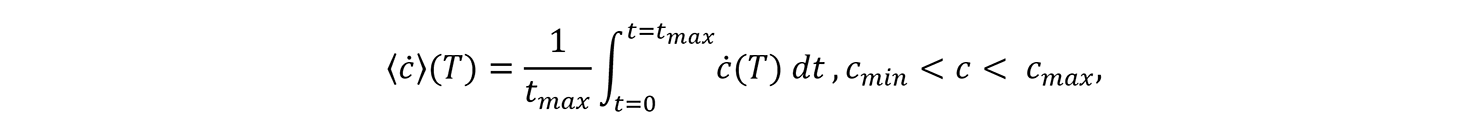
onde ċ é a velocidade de cura atual. A restrição a um grau de cura máximo e mínimo assegura que apenas a reação de cura é tida em conta. O tempo antes e depois da actual reação de cura é descartado no cálculo. A velocidade média de cura captura a taxa dependente da temperatura de cura durante o processo de vulcanização. No caso de temperaturas constantes, a velocidade média de cura simplifica a inclinação da fase de secante desde o início da reação de cura até ao seu fim.

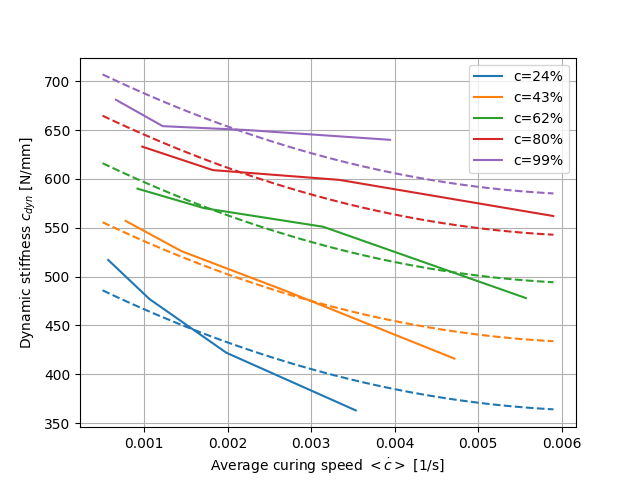
A velocidade média de cura é calculada para cada temperatura e grau de cura indicado a partir de Figura 3, e a rigidez dinâmica é agora traçada sobre o grau de cura e a velocidade média de cura (ver Figura 4). Pode observar-se uma correlação monotónica entre a rigidez dinâmica e tanto o grau de cura como a velocidade média de cura.

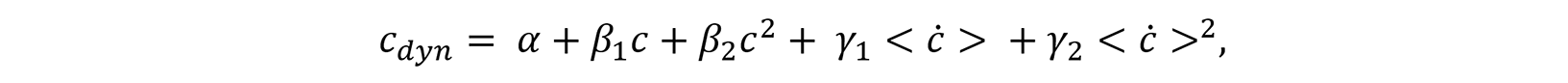
Estes parâmetros têm de ser ajustados de modo a que o modelo reproduza os dados da Figura 4 de forma ótima. Isto leva a um coeficiente de determination〖 R〗^2=95% (ver Figura 5).

O grau de cura estabelecido localmente e a velocidade média de cura de uma simulação de processo podem agora ser utilizados como um input para este novo modelo. Como resultado, é calculada a rigidez dinâmica localmente resolvida, que substitui os parâmetros mecânicos anteriormente homogéneos para a análise estrutural.

Nesta contribuição, a rigidez dinâmica é um exemplo de uma possível propriedade mecânica. O mesmo procedimento aplica-se igualmente a outras propriedades mecânicas (módulo de Young, o conjunto de compressão, etc.).

A pressuposição de parâmetros mecânicos homogéneos na análise estrutural limita a sua precisão alcançável. As experiências mostraram que dois fatores do processo dominam as propriedades mecânicas, nomeadamente o grau de cura e a velocidade média de cura. Assim, as propriedades mecânicas localmente resolvidas para a análise estrutural de alta qualidade só podem ser obtidas a partir da simulação do processo.

Foi apresentado um novo procedimento de medição, bem como um novo modelo que correlaciona as condições de processo e as propriedades mecânicas da peça final e o algoritmo de encaixe necessário para os parâmetros materiais exigidos. O cálculo do grau de cura, da velocidade média de cura e dos parâmetros mecânicos desejados para a análise estrutural estão perfeitamente integrados no software de simulação de moldação por injeção Sigmasoft.

¹ Weinhold G., Modelar a influência do processo de moldagem por injecção nas propriedades mecânicas, DKT (2021)